Американські та японські фізики закрутили під близьким до магічного кутом «сендвіч» з двох шарів графену та побачили, що умови появи надпровідності в ньому не збігаються з передбаченнями теорії Бардіна — Купера — Шріффера, що описує традиційні надпровідники. На думку вчених, надпровідність двошарового графену слід пояснювати структурою його електронних зон, що впливає на поведінку носіїв заряду. Вони сподіваються, що їхнє дослідження допоможе і теоріям, що пояснюють фізику високотемпературних надпровідників. Стаття опублікована у Nature.
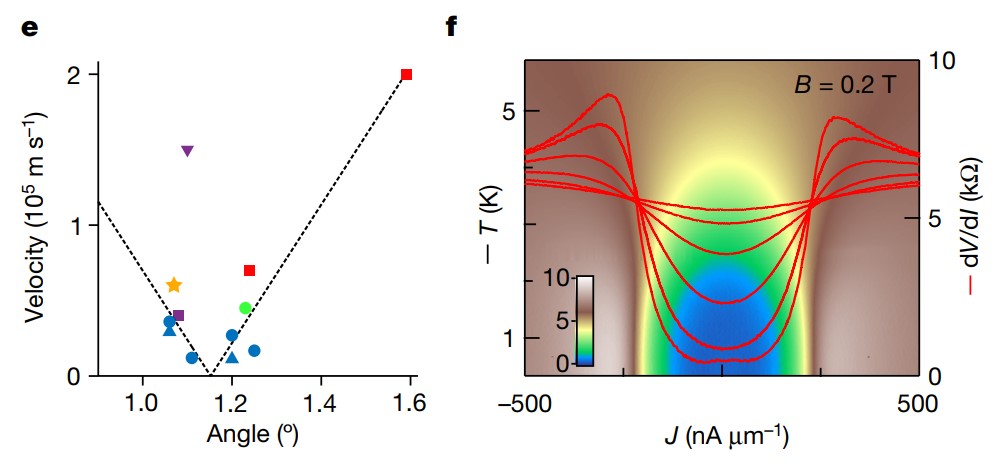
Розрахована швидкість носіїв заряду для двошарового графену (експериментальні дані позначені блакитним) (е); залежність опору графенового зразка від температури, за зниження якої він різко падає (f). Haidong Tian et al. / Nature, 2023
Звідки береться надпровідність?
Появу надпровідності, тобто здатності проводити струм без опору, у кількашаровому графені пояснюють його електронною структурою, яку можна уявити як конус (конус Дірака), у вершинах якого знаходяться переходи між валентною зоною і зоною провідності для електронів. При повороті шарів «сендвіча» під певним (фізики ще називають його магічним) кутом, конуси Дірака утворюють площину, в якій швидкість Фермі носіїв заряду знижується до нуля, а графеновий «сендвіч» за температури у кілька кельвінів перетворюється на надпровідник.
Втім, поведінку електронів у двошаровому графені цілком пояснити теорією Бардіна — Купера — Шріффера (БКШ), що вважається провідною у мікроскопічною теорією надпровідності, не вдається. Розбіжності з нею знайшли і фізики зі США та Японії, досліджуючи надпровідність у двошаровому графені.
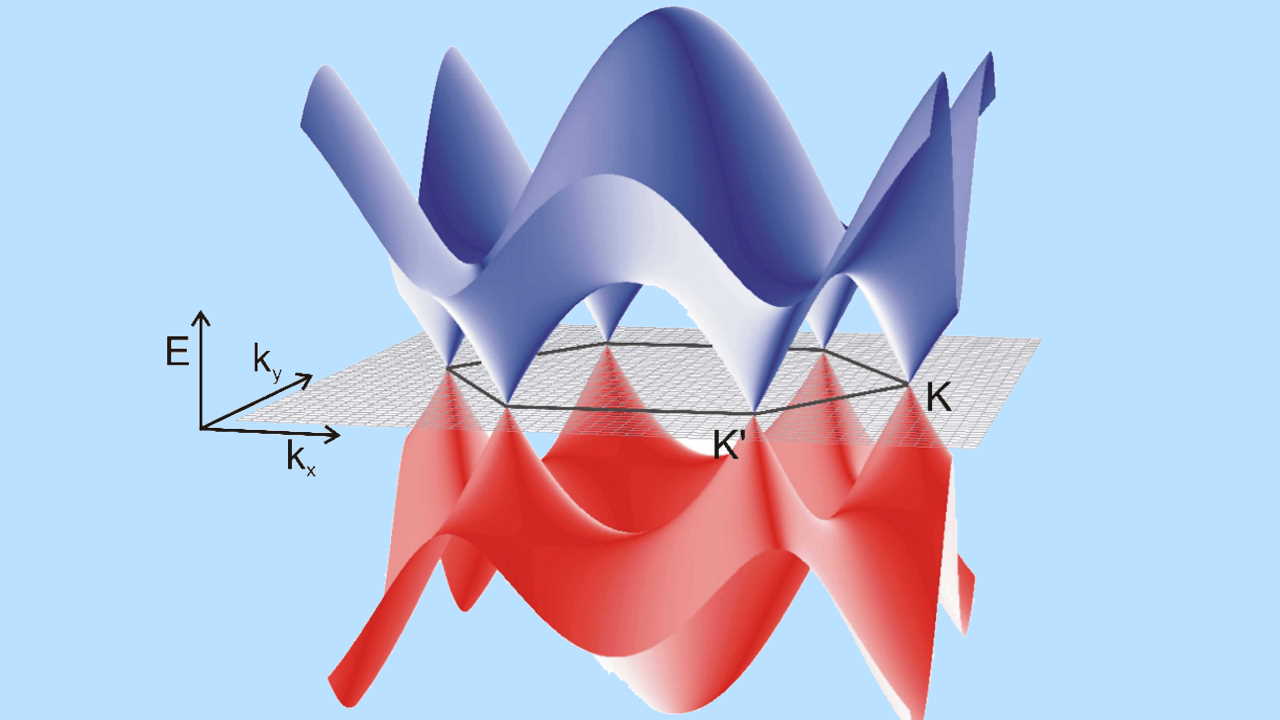
Схематичне зображення зонної структури графену з вершинами конусів Дірака в К і К`. Milan Orlita et al.
Яку надпровідність отримали вчені?
За температури 0,3 кельвіна зразок графену дослідників став виявляти надпровідні властивості за значення рівня заселеності електронів ν −5/8 ≤ ν ≤ −1/2. Швидкість Фермі носіїв заряду склала приблизно 1 000 метрів на секунду, що менше, ніж у звичайному графені, та, як вважають дослідники, пов'язано з тим, що вони закрутили шари графену під кутом у 1,08 градуса, що близьке до магічного значення в 1,1 градуса. Згідно з теорією БКШ, критична температура, за якої опір у графені мав би зрости до 20 відсотків від значення спротиву у звичайному (не надпровідному) стані, склала б 0,05 кельвіна. Тоді як в експериментах фізики отримали значення у 2,2 кельвіна.
На думку дослідників, за надпровідність у їхньому зразку, відповідає геометрія хвильових функцій його електронів, що впливає на надплинну жорсткість (superfluid weight) — визначальну характеристику електромагнітного відгуку надпровідника. Вона напряму пов'язана з критичною температурою надпровідного переходу, а робота вчених свідчить, що її нижня межа пов'язана з геометрією електронних зон у надпровіднику, яка дає носіям заряду змогу навіть за низької швидкості Фермі виявляти надпровідну поведінку.
Експериментальні дані фізиків у дослідженні збіглися з їхніми розрахунками. Вони сподіваються, що їхня робота допоможе краще зрозуміти природу надпровідності не лише у графені, а і у високотемпературних надпровідниках, для опису якої теорія БКШ також наразі не підходить.
Раніше ми розповідали, як стабільності надпровідності у графені посприяла більша кількість його шарів, що, імовірно, впливає на заповненість пласкої зони, що утворюється з конусів Дірака у графені.